Aerodynamics
Physics of Aerodynamic Flight
Pioneer simulates aerodynamic drag and lift in a relatively simple manner. All non-ship dynamic objects (missiles, cargo etc.) are considered to be perfect spheres in the drag equation.
drag_force = 0,5 * atmospheric_pressure * velocity^2 * drag_constant
Drag constant for sphere is 0,1.
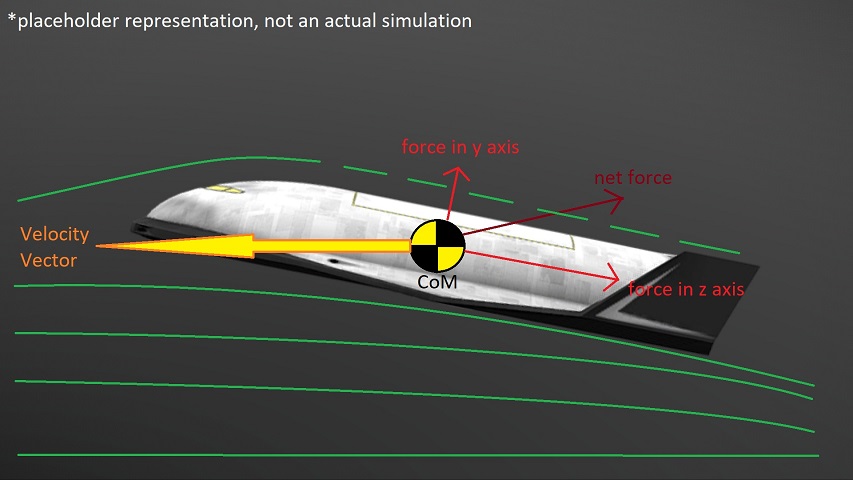
The drag values for ships are calculated separately for each axis (local to the ship), by getting the ship's cross section for each axis. Each ship has it's cross section area values in their respective .json files, in meters squared.
Sum of all forces in three axises allow ships to generate lift and/or manuever by increasing their angle of attack. Pioneer simulates non-cambered wings, with equal air displacement on either side of AoA.
Pioneer also simulates stall. If the angle of attack is too high, the airflow will get disrupted, resulting in loss of lift force. With the current simulation (wiki updated at 22 September 2019), generated lift peaks at around 20 degrees, and falls off fully at 35-ish. However, this is relatively poorly simulated and probably needs to be swapped with a curve-based implementation in the future.
Aerodynamic Stability
Most spacecraft in Pioneer are passively stable in atmosphere, forcing a nose-first orientation by generating torque while travelling in atmosphere. The strenght of this force is highly ship-specific, and better aerodynamic designs (like Wave and Deneb) are more stable compared to non-aerodynamic ships (like DSMiner). However, just like the case of AoA simulation, this is rather poorly simulated and probably needs some change in the future.
While making a new ship, or assessing an existing ship's stability, the most useful information is the Center of Mass (CM) and the Center of Pressure (CP) of the vessel. A ship in airflow tends to go CM-first into the flow, and CP tends to trail the Center of Mass. If this is not satisfied, the unbalanced dynamic pressure will create a "righting moment" that tries to force the vehicle into a CM-first orientation. Imagining a straight line from CP to CM, there are two equilibrium flight configurations (so that no righting force is applied);
The CP-CM line is aligned with the airflow, flying CM-first (Stable Equilibrium)
The CP-CM line is aligned with the airflow, flying CP-first (Unstable Equilibrium)
The righting torque is maximum when the CP-CM line is making a 90 degree angle to the airflow, and zero at either equilibrium. But, in the case of flying backwards (CP-first), a slight deviation from the alignment, unless actively cancelled by control systems, will result in the ship forcibly turning to the stable equilibrium orientation (whereas in the stable equilibrium case, the righting moment will work to cancel the deviation.)
If you are familiar with any of them, this concept is kind of similar to how electric dipoles orient themselves in electric fields, or how ships right themselves with their Center of Mass and Center of Buoyancy.
The exact righting moment applied increases with airflow velocity and the separation between the CM and CP. To assign an "aero_stability" value to a ship in its JSON definition, the most important metric is the distance between the model's origin (which is the point about which the ship rotates, therefore acting as the CM) and the center of geometry of the spacecraft (acting as the CP).
If you want to see a simple illustration: https://www.grc.nasa.gov/WWW/k-12/rocket/rktstab.html
Aerodynamic Manuevers
(Could be moved to it's own tutorial page?)
If the atmospheric pressure is good enough, the current simulation model allows aerodynamic spacecraft to move like airplanes (go where you are pointing at.)
By carefully increasing and decreasing the perpendicular area to the velocity vector, pilots can perform very precise aerobraking manuevers. This also makes managing the atmospheric entry heat much easier.
The current aerodynamic flight simulation could, in theory, allow pilots to perform an aerogravity assist. (https://en.wikipedia.org/wiki/Aerogravity_assist)